I've cleaned up the schematics a bit. This is the version with linear vca and resonance CVs, 10 modes, overdrive and possibly oscillation issues. It may change in the future.
Monday, January 28, 2019
Jupiter 6 All pass filter
This post
https://www.muffwiggler.com/forum/viewtopic.php?t=137105&start=all&postdays=0&postorder=asc&sid=3ef1fe17aeeff7d7fd87444b7188ac69
mentions that by mixing the input with 2 x the BP filter, you'll get an all pass filter. The same does this pdf:
https://www.analog.com/media/en/training-seminars/tutorials/MT-223.pdf
I tried this with some success. I had to disconnect the 33k resonance resistor, but after this I got a response with a slight 667 mdB notch.
I will try breadboarding this later.
The MT-223-pdf also mentions an alternative way of doing a notch filter:
Which gives this notch:
As opposed to the notch we get by mixing LP and HP:
https://www.muffwiggler.com/forum/viewtopic.php?t=137105&start=all&postdays=0&postorder=asc&sid=3ef1fe17aeeff7d7fd87444b7188ac69
mentions that by mixing the input with 2 x the BP filter, you'll get an all pass filter. The same does this pdf:
https://www.analog.com/media/en/training-seminars/tutorials/MT-223.pdf
I tried this with some success. I had to disconnect the 33k resonance resistor, but after this I got a response with a slight 667 mdB notch.
I will try breadboarding this later.
The MT-223-pdf also mentions an alternative way of doing a notch filter:
Which gives this notch:
As opposed to the notch we get by mixing LP and HP:
Sunday, January 27, 2019
OTA filter cell
Fun fact - after looking for an explanation for the OTA used in the juno for a couple of years, I found it in my bookshelf because someone mentioned a circuit in the Musical Applications for Microprocessors book by Hal Chamberlin.
When trying to understand a circuit, I often look for visually similar circuits, but even though I have found several OTA filters, they are always different from the Juno one. But here is the clue: These are similar:
The left one is what you find in the Roland schematics, the right one is found in papers and OTA filter explanations elsewhere. It is explained in some detail in the section on voltage controlled filters, page 201 and onwards in 'Musical Applications for Microprocessors'.
The cell is really quite simple - the resistors, 68k and 560Ohm function as voltage dividers to reduce the input signal to the OTA. This is true for both the 68k on the input and the 68k in the feedback loop.
When trying to understand a circuit, I often look for visually similar circuits, but even though I have found several OTA filters, they are always different from the Juno one. But here is the clue: These are similar:
 |
| The typical Roland filter cell to the left, its equivalent to the right. |
The cell is really quite simple - the resistors, 68k and 560Ohm function as voltage dividers to reduce the input signal to the OTA. This is true for both the 68k on the input and the 68k in the feedback loop.
Jupiter 6 filter - overdrive and multiple output variations
Overdrive
With a 3.9k input gain feedback resistor I could easily pass a 20V p.p. wave through the filter without distortion. But I wanted to see if I could get a distortion similar to the moog filter, and yes, I could.
Swapping the 3.9k resistor with a 33k makes the filter overdrive close to 10V p.p, quite similar to the Moog.
This is of course pre-filter amplification. I have seen people talking about the minimoog doing feedback of the original signal through the external input jack, and this sounding better, so I'll try that next. I also need to come up with a good way to control overdrive, one that is not so dependent on input amplitude.
Output variations
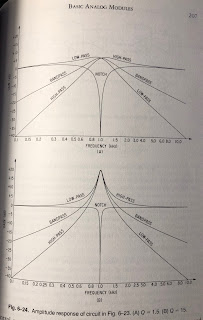
This being a state variable filter means it can produce a multitude of filter variations at the same time - low pass, band pass, high pass and notch. It is also two filters after one another, which means we can get various falloff. I've played around with this and come up with 10 variations that are more or less usefull:
12dB LP
24dB LP
12dB HP
24dB HP
6dB BP + 12dB LP
6dB BP + 12dB HP
Notch (first SVF)
Notch + LP
Notch + HP
Notch + BP
I am not sure of the usefullness of all these but the cost to add them all is very little. Here is how I indend to wire them, with resistor values giving the following 'plateau' gain.
Constant current inputs
Just like with the Juno and Moog filters, I've swapped the resonance and vca gain CV circuits for my own, linear designs. The VCA gain control is exactly the same as for the Juno (but with slightly different part values), and has a similar deadband. The resonance on the other hand, is different. The resonance circuit works opposite of the one in the Juno, increasing the resonance OTA gain reduces the amount of resonance.
Because of this, increasing CV must decrease the output current. Also, when doing exponential conversion in software later, we must generate a negative exponentially decaying signal instead of an exponentially increasing one, which is too bad as it means that we cannot have a common control system for all filters. I will have to look closer into this.
Oh, and because of the way I did the linear control, we don't get a deadband.
With a 3.9k input gain feedback resistor I could easily pass a 20V p.p. wave through the filter without distortion. But I wanted to see if I could get a distortion similar to the moog filter, and yes, I could.
Swapping the 3.9k resistor with a 33k makes the filter overdrive close to 10V p.p, quite similar to the Moog.
This is of course pre-filter amplification. I have seen people talking about the minimoog doing feedback of the original signal through the external input jack, and this sounding better, so I'll try that next. I also need to come up with a good way to control overdrive, one that is not so dependent on input amplitude.
 |
| Input (green) vs output (blue). 33k input resistor, 50k output pot |
Output variations
This being a state variable filter means it can produce a multitude of filter variations at the same time - low pass, band pass, high pass and notch. It is also two filters after one another, which means we can get various falloff. I've played around with this and come up with 10 variations that are more or less usefull:
12dB LP
24dB LP
12dB HP
24dB HP
6dB BP + 12dB LP
6dB BP + 12dB HP
Notch (first SVF)
Notch + LP
Notch + HP
Notch + BP
I am not sure of the usefullness of all these but the cost to add them all is very little. Here is how I indend to wire them, with resistor values giving the following 'plateau' gain.
Constant current inputs
Just like with the Juno and Moog filters, I've swapped the resonance and vca gain CV circuits for my own, linear designs. The VCA gain control is exactly the same as for the Juno (but with slightly different part values), and has a similar deadband. The resonance on the other hand, is different. The resonance circuit works opposite of the one in the Juno, increasing the resonance OTA gain reduces the amount of resonance.
Because of this, increasing CV must decrease the output current. Also, when doing exponential conversion in software later, we must generate a negative exponentially decaying signal instead of an exponentially increasing one, which is too bad as it means that we cannot have a common control system for all filters. I will have to look closer into this.
 |
| CV vs I_abc for one resonance OTA, original Jupiter 6 circuit. With a linear response, a similar CV curve must be calulated in software. |
Oh, and because of the way I did the linear control, we don't get a deadband.
Jupiter 6 filter - oscillation issue
I did a lot more work on the Jupiter 6 filter today.
First of all, I tried figuring out why I get oscillation on the input whenever cutoff CV was above 4.7V.
I have yet to figure out what is going on, but I tried replacing all ideal opamps with TL072 simulations and I still have the issue. I will have to breadboard the circuit to see if it is real or not.
But even so, there are a few things that make this happen:
1) When resonance CV is at 0V, I get oscillation if cutoff CV > 4.7 and input gain feedback resistor > 3.9k. With 4.7V CV I could use at least a 15k resistor without problems.
2) Decreasing the 33k resistor from input to the resonance OTA, or removing the line completely, fixes the problem
3) Increasing resonance also removes the issue.
All in all, it seems that anything that makes MORE current pass through the circuit causes this oscillation. I tried quickly reading up on op amp oscillation but no quick remedy was found. I also cut down on the circuit to the point where only the first SVF with constant current controls (no expo converters etc) and no output VCA was left and still had the issue.
First of all, I tried figuring out why I get oscillation on the input whenever cutoff CV was above 4.7V.
I have yet to figure out what is going on, but I tried replacing all ideal opamps with TL072 simulations and I still have the issue. I will have to breadboard the circuit to see if it is real or not.
But even so, there are a few things that make this happen:
1) When resonance CV is at 0V, I get oscillation if cutoff CV > 4.7 and input gain feedback resistor > 3.9k. With 4.7V CV I could use at least a 15k resistor without problems.
2) Decreasing the 33k resistor from input to the resonance OTA, or removing the line completely, fixes the problem
3) Increasing resonance also removes the issue.
All in all, it seems that anything that makes MORE current pass through the circuit causes this oscillation. I tried quickly reading up on op amp oscillation but no quick remedy was found. I also cut down on the circuit to the point where only the first SVF with constant current controls (no expo converters etc) and no output VCA was left and still had the issue.
Thursday, January 24, 2019
State variable filters, some quick resources
I found these resources while trying to understand how resonance defeat works in a state variable filter:
A very good general description
https://www.electronics-tutorials.ws/filter/state-variable-filter.html
Some more about gain and stuff
Says that passband gain should not be affected by Q (resonance)
http://sound.whsites.net/articles/state-variable.htm
All pass and equations
https://www.analog.com/media/en/training-seminars/tutorials/MT-223.pdf
Musical Applications of Microprocessors
Then I found this on a forum (which I unfortunately forgot to bookmark):
I first read about how SVFs work in Hal Chamberlin's book, Musical Applications of Microprocessors , where there's a lovely diagram of the filter's structure. I later spotted that same diagram in an article about an analogue computer. Apparently an SVF and a physical model of a spring have the same structure! Well, they're both dynamic systems that resonate, so I shouldn't be too suprised if they share the same mathematics.
Incidently I have this in my bookshelf, so I checked it, and it did indeed have a good diagram. But even better - it had an implementation using CA3080, which is almost exactly identical to the one in the Jupiter 6!
It's the first time I have come across that implementation, it even says that the capacitor-to-ground between the OTA and the buffer equals the configuration with the capacitor in the feedback loop of an opamp that I have seen elsewhere. Oh - and the book is from 1980, three years before the JP6 came on the market.
This one has both BP and band reject/notch. Oh, and it is missing the resistor i talked about in a previous post and has no change in gain for frequencies below the resonance frequency.
Matrix 12
I also looked at the Matrix 12 filter. It is NOT a state variable filter, it is a multimode filter, which mixes the output from four poles in various gain/variations to get 15 different responses. This matches well with what MT-223 above says about mixing different gains.
Cem chip used in the Matrix 12, CEM3372
https://pdf1.alldatasheet.com/datasheet-pdf/view/95160/ETC/CEM3372.html
A very good general description
https://www.electronics-tutorials.ws/filter/state-variable-filter.html
Some more about gain and stuff
Says that passband gain should not be affected by Q (resonance)
http://sound.whsites.net/articles/state-variable.htm
All pass and equations
https://www.analog.com/media/en/training-seminars/tutorials/MT-223.pdf
Musical Applications of Microprocessors
Then I found this on a forum (which I unfortunately forgot to bookmark):
I first read about how SVFs work in Hal Chamberlin's book, Musical Applications of Microprocessors , where there's a lovely diagram of the filter's structure. I later spotted that same diagram in an article about an analogue computer. Apparently an SVF and a physical model of a spring have the same structure! Well, they're both dynamic systems that resonate, so I shouldn't be too suprised if they share the same mathematics.
Incidently I have this in my bookshelf, so I checked it, and it did indeed have a good diagram. But even better - it had an implementation using CA3080, which is almost exactly identical to the one in the Jupiter 6!
It's the first time I have come across that implementation, it even says that the capacitor-to-ground between the OTA and the buffer equals the configuration with the capacitor in the feedback loop of an opamp that I have seen elsewhere. Oh - and the book is from 1980, three years before the JP6 came on the market.
This one has both BP and band reject/notch. Oh, and it is missing the resistor i talked about in a previous post and has no change in gain for frequencies below the resonance frequency.
Matrix 12
I also looked at the Matrix 12 filter. It is NOT a state variable filter, it is a multimode filter, which mixes the output from four poles in various gain/variations to get 15 different responses. This matches well with what MT-223 above says about mixing different gains.
Cem chip used in the Matrix 12, CEM3372
https://pdf1.alldatasheet.com/datasheet-pdf/view/95160/ETC/CEM3372.html
On bandwidth vs Q:
Jupiter 6 filter resonance gain
When I first simulated the jupiter filter, I had made a mistake. I forgot to connect a 33k resistor from the negative terminal of the resonance OTA and to the filter input. I didn't notice, and all my plots looked good. More than that - I actually could add resonance without the lower frequencies getting attenuated. Reading up on state variable filters today indicates that this is a feature of this filter topology (http://sound.whsites.net/articles/state-variable.htm)
When I corrected this error though, to my great surprise, lower frequencies got heavily attenuated once resonance went up!
I have checked and rechecked and traced the original JP6 PCB but I always come to the same conclusion - the resistor is there.
I even went back and simulated the filter with and without the resistor, looking at both filter response and phase, and honestly, I can't see ANY difference, except for the attenuation.
This begs the question: What is the purpose of this resistor/line?
Right now my only two conclusions are either that it is there to attenuate lower frequencies on purpose - exactly the thing other filter designers fight to. Or LTspice simulates the circuit incorrectly.
I guess won't get an answer to the last question until I breadboard the circuit.
Update: Scott Bernardi made a comment about the attenutation here: http://www.bernacomp.com/elec/og2/og3_4pmultimode.html - Without it the resonance would start clipping (depending on the rest of the circuit of course). That makes sense.
When I corrected this error though, to my great surprise, lower frequencies got heavily attenuated once resonance went up!
I have checked and rechecked and traced the original JP6 PCB but I always come to the same conclusion - the resistor is there.
I even went back and simulated the filter with and without the resistor, looking at both filter response and phase, and honestly, I can't see ANY difference, except for the attenuation.
 |
| Zero resonance without resistor |
 |
| Zero resonance with resistor |
 |
| Max resonance without resistor, same low frequency gain as no resonance |
 |
| Max resonance with resistor. gain has fallen by 24dB |
This begs the question: What is the purpose of this resistor/line?
Right now my only two conclusions are either that it is there to attenuate lower frequencies on purpose - exactly the thing other filter designers fight to. Or LTspice simulates the circuit incorrectly.
I guess won't get an answer to the last question until I breadboard the circuit.
Update: Scott Bernardi made a comment about the attenutation here: http://www.bernacomp.com/elec/og2/og3_4pmultimode.html - Without it the resonance would start clipping (depending on the rest of the circuit of course). That makes sense.
Jupiter 6 filter resonance
I'm feeling fairly satisfied with the Juno and Moog filters now, so it's time to do another round with the JP6 filter.
The cutoff control is not that interesting, I assume I can tweak the starting point just the same way I did with the two others, and reuse the expo converter from the Juno - after all, the filter core should function the same way, with a doubling in control current resulting in a doubling of frequency.
The resonance on the other hand, is completely different. The juno returns the difference of the filter output and filter input, tapped at the last stage, and returns it to the start of the filter. The jp6 on the other hand, returns the SUM of the output of the first stage and the filter input and returns it to the start of the filter, where it is also mixed with the output of the second stage.
I discovered quite early on that reusing the resonance control from the Juno filter did not work as it should. In fact, I got resonance with a 0V input and the resonance fell when increasing the CV. At last 10V was needed for a 'normal' response without resonance.
I went back to the datasheet, and discovered that the resonance OTAs are actually IR3109s, which means that they have built in exponential converters. This makes a huge difference of course. I went on to duplicate the expo converter from the juno filter, after all it should be a close approximation of the one from the IR3109, and add the rest of the JP6 control circuit. I also re-read the datasheet and it seems the JP6 DAC outputs up to 10.7V (see page 4b, DAC amplitude). Finally, each resonance CV feeds two voices and each voice has two resonance OTAs (In fact, two voices share one IR3109), so I added two additional OTAs to the simulation to get a correct split for the I_abc.
So far so good. But the OTA CV circuit has a trimmer in it. And this trimmer has a huge effect on not only how high the resonance peak gets, but on how little resonance we get too.
In the Juno filter, fully turning off the resonance OTA meant no resonance. In the JP6 on the other hand, there is no absolute 'no resonance' point. The OTAs 'defeat' resonance by feeding back more of the output of the first stage (and third stage), so turning it off means maximum resonance.
Here are some plots. First of the resonance CV from 0 to 10.7V and the corresponding I_abc current for each OTA. We can clearly see that the lower the CV, the higher the current - and higher I_abc means a higher gain in the OTA. There are three plots, each for a resonance trimmer setting of 0, 0.5 and 1 (wiper position).
Second series of plots show the corresponding frequency response is. Note that for a trimmer setting of 1, A 0V CV still results in a quite visible resonance. Wiper at 0 or 0.5 shows no bump, but which one is the correct one? Or is it somewhere in between?
Finally, a plot of trimmer position vs minimum resonance. The top green line is wiper at 0. All lines after the grey one (wiper at 0.5) shows a bump so they are definitely not correct, but are any of the others?
My conclusion then, which I guess is ultimately quite fun, is that I have to understand what is going on. How does this filter create resonance, and what exactly is it that the OTA output defeats. When knowing that, I can go back and calculate what the best output of the OTA is, and get the necessary theoretical gain.
OBTW: Why bother? Why not use the circuit like it is? Well, for one I would not know how to properly calibrate it, and second, I think I still like to keep the resonance control linear and do the expo conversion in software, the way the other filters do.
UPDATE: I tried reading up on Q, resonance etc. It is not easily understood exactly how it comes about. But I DID find some great reasources on state variable filters, that inspired me to try adding more features - tapping bandpass after pole 1 and 3 (6dB) and creating notch / AP versions. Very exciting!
I ended up doing a quite crude comparison of the falloff between the Juno and Jupiter filters. I positioned a marker at resonance frequency and then measured the falloff from the 'plateau' down to it. I found the dropoff to be about 10.3dB and so I have adjusted the Jupiter filter to match this when the resonance CV is 0V by setting the resonance offset trimmer U23 to 0.25.
The cutoff control is not that interesting, I assume I can tweak the starting point just the same way I did with the two others, and reuse the expo converter from the Juno - after all, the filter core should function the same way, with a doubling in control current resulting in a doubling of frequency.
The resonance on the other hand, is completely different. The juno returns the difference of the filter output and filter input, tapped at the last stage, and returns it to the start of the filter. The jp6 on the other hand, returns the SUM of the output of the first stage and the filter input and returns it to the start of the filter, where it is also mixed with the output of the second stage.
I discovered quite early on that reusing the resonance control from the Juno filter did not work as it should. In fact, I got resonance with a 0V input and the resonance fell when increasing the CV. At last 10V was needed for a 'normal' response without resonance.
I went back to the datasheet, and discovered that the resonance OTAs are actually IR3109s, which means that they have built in exponential converters. This makes a huge difference of course. I went on to duplicate the expo converter from the juno filter, after all it should be a close approximation of the one from the IR3109, and add the rest of the JP6 control circuit. I also re-read the datasheet and it seems the JP6 DAC outputs up to 10.7V (see page 4b, DAC amplitude). Finally, each resonance CV feeds two voices and each voice has two resonance OTAs (In fact, two voices share one IR3109), so I added two additional OTAs to the simulation to get a correct split for the I_abc.
So far so good. But the OTA CV circuit has a trimmer in it. And this trimmer has a huge effect on not only how high the resonance peak gets, but on how little resonance we get too.
Here are some plots. First of the resonance CV from 0 to 10.7V and the corresponding I_abc current for each OTA. We can clearly see that the lower the CV, the higher the current - and higher I_abc means a higher gain in the OTA. There are three plots, each for a resonance trimmer setting of 0, 0.5 and 1 (wiper position).
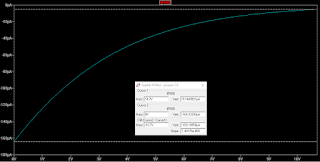 |
| Wiper at 0 |
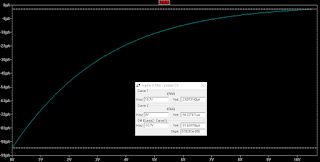 |
| Wiper at 0.5 |
 |
| Wiper at 1 |
 |
| Wiper at 0 |
 |
| Wiper at 0.5 |
 |
| Wiper at 1 |
Finally, a plot of trimmer position vs minimum resonance. The top green line is wiper at 0. All lines after the grey one (wiper at 0.5) shows a bump so they are definitely not correct, but are any of the others?
My conclusion then, which I guess is ultimately quite fun, is that I have to understand what is going on. How does this filter create resonance, and what exactly is it that the OTA output defeats. When knowing that, I can go back and calculate what the best output of the OTA is, and get the necessary theoretical gain.
OBTW: Why bother? Why not use the circuit like it is? Well, for one I would not know how to properly calibrate it, and second, I think I still like to keep the resonance control linear and do the expo conversion in software, the way the other filters do.
UPDATE: I tried reading up on Q, resonance etc. It is not easily understood exactly how it comes about. But I DID find some great reasources on state variable filters, that inspired me to try adding more features - tapping bandpass after pole 1 and 3 (6dB) and creating notch / AP versions. Very exciting!
I ended up doing a quite crude comparison of the falloff between the Juno and Jupiter filters. I positioned a marker at resonance frequency and then measured the falloff from the 'plateau' down to it. I found the dropoff to be about 10.3dB and so I have adjusted the Jupiter filter to match this when the resonance CV is 0V by setting the resonance offset trimmer U23 to 0.25.
 |
| Juno filter |
 |
| Jupiter filter |
Monday, January 21, 2019
Juno and moog filter simulations for ltspice
I've uploaded the latest filter simulations:
Juno filter https://xonik.github.io/xm8/filters/juno/Xonik XM8 OTA filter.asc
Moog ladder filter https://xonik.github.io/xm8/filters/moog/Xonik XM8 ladder filter.asc
LM13700 OTA: https://xonik.github.io/xm8/filters/juno/LM13700.asy
Potentiometer: https://xonik.github.io/xm8/filters/juno/potentiometer_standard.asy
Juno filter https://xonik.github.io/xm8/filters/juno/Xonik XM8 OTA filter.asc
Moog ladder filter https://xonik.github.io/xm8/filters/moog/Xonik XM8 ladder filter.asc
LM13700 OTA: https://xonik.github.io/xm8/filters/juno/LM13700.asy
Potentiometer: https://xonik.github.io/xm8/filters/juno/potentiometer_standard.asy
Moog ladder filter revised
After all the work I did on improving the range and controls of the Juno filter, I decided to have a closer look at the Moog filter. I have improved the following:
In addition to all this, I've completely changed the signal attenuation/gain to enable overdriving.
Overdrive
The Memorymoog schematics indicates that a 40mV p.p. at the transistor base of the bottom ladder transistor is the 'norm'. My simulations show severe distortion at this level. I could see distortion all the way down to 10mV p.p. I have suggested three component values that will work for 5, 10 and 20V p.p. input (with a 15mV p.p. base voltage at those values). This gives a slight distortion at the highest inputs, and further distortion should the input exceed the specification. For example, a 10V p.p wave maxes out at about 16V p.p even with much higher input.
How the overdrive sounds in practice is still unknown.
Computer calibration
It would probably be possible to tune most parameters of the filter using lookup tables in the computer control. Here are some thoughts on that:
- If no deadband is needed (i.e. 0V input to the VCA CV gives an 'off' output), the U17 trim pot and R41 may removed. Keeping R41 but connecting it to -15, and changing the value to 1.5MOhm will give a 100mV deadband.
- The U13 VCA gain potentiometer can be replaced with a fixed resistor that gives a more-than-unity gain at max CV. By doing this, the VCA CV can be calculated in software to give a correct curve with a end point that results in unity gain.
- Similarly, U20 can be chosen in such way that it results in a resonance higher than what is wanted, and CV then corrected in software for max resonance.
- I would probably still keep the tracking potentiometer, but R36 can be replaced with a lower value, giving a lower frequency as a starting point. Then you could replace R32 with a 25k resistor to get 20 octaves of CV control, enabling proper calibration of lowest and highest cutoff.
- It IS also possible to replace the tracking pot U9 and resistor R23 with a 100k resistor. Tracking could then be adjusted in software.
- VCA CV is now similar to the Juno - it has an adjustable deadband at the start and a summing point for multiple CVs
- Resonance CV is similar to the Juno in the same way
- Cutoff CV summer has been altered to give a 10Hz cutoff from a 0V CV, with +/- 5.6 octaves trimability, fairly similar to the Juno.
- I have added a tempco resistor to the exponential converter.
- I have added an option to tap the audio output at 12dB/oct instead of 24. Resonance is still tapped at 24dB to get a nice high resonance. No switch has been drawn but either an electronic or mechanical DPDT switch will do.
- I replaced the output buffer with a transinductance circuit and instead flipped the inputs to the VCA OTA to keep phase. This fixed the maximum cutoff frequency similarly to the Juno.
- I added a linear FM input to the cutoff frequency.
In addition to all this, I've completely changed the signal attenuation/gain to enable overdriving.
Overdrive
The Memorymoog schematics indicates that a 40mV p.p. at the transistor base of the bottom ladder transistor is the 'norm'. My simulations show severe distortion at this level. I could see distortion all the way down to 10mV p.p. I have suggested three component values that will work for 5, 10 and 20V p.p. input (with a 15mV p.p. base voltage at those values). This gives a slight distortion at the highest inputs, and further distortion should the input exceed the specification. For example, a 10V p.p wave maxes out at about 16V p.p even with much higher input.
How the overdrive sounds in practice is still unknown.
 |
| Input (blue) vs output (green), input is 8V to 30V p.p |
Computer calibration
It would probably be possible to tune most parameters of the filter using lookup tables in the computer control. Here are some thoughts on that:
- If no deadband is needed (i.e. 0V input to the VCA CV gives an 'off' output), the U17 trim pot and R41 may removed. Keeping R41 but connecting it to -15, and changing the value to 1.5MOhm will give a 100mV deadband.
- The U13 VCA gain potentiometer can be replaced with a fixed resistor that gives a more-than-unity gain at max CV. By doing this, the VCA CV can be calculated in software to give a correct curve with a end point that results in unity gain.
- Similarly, U20 can be chosen in such way that it results in a resonance higher than what is wanted, and CV then corrected in software for max resonance.
- I would probably still keep the tracking potentiometer, but R36 can be replaced with a lower value, giving a lower frequency as a starting point. Then you could replace R32 with a 25k resistor to get 20 octaves of CV control, enabling proper calibration of lowest and highest cutoff.
- It IS also possible to replace the tracking pot U9 and resistor R23 with a 100k resistor. Tracking could then be adjusted in software.
Tuesday, January 15, 2019
Juno filter: cap values and expo converter musings
After spending the last few weeks experimenting with the Juno filter, I have some thoughts. It seems the exact compnent values along the signal path are not terribly important to how the filter works. A lot of the filter is tweakable as we've seen in my previous posts - the input CV ranges, the VCA gain etc.
I have tried various cap values as well, and today I made a comparison of both cap values and changes to the expo converter.
Expo converter
The expo converter core is dependent on a reference current. Right now that is set up using a 1.5MOhm resistor, but changing this does not change the output curve, it only changes WHAT linear CV gives what output.
I tried swapping for a 1MOhm resistor, and using the base octave trimmer I could still get the necessary output range. Here are the currents through a single I_abc resistor:
Using 1.5MOhm resistor, the output current is:
Full trim and 5V CV range: 3.2nA to 1.377mA
Center trimmed: 165nA to 168uA
Using 1MOhm resistor, the output current is:
Full trim and 5V CV range: 4.9nA to 1.379mA
Center trimmed: 248nA to 238uA
The Juno 106 uses 240pF caps, other Roland synths use 330pF, and we use 270pF. Here are the responses to a center trimmed CV using a 1.5MOhm reference resistor:
240pF
0V = 7.7Hz
5V = 6.4kHz
10V = 42kHz
270pF:
0V = 7Hz
5V = 5.7kHz
10V = 39kHz
330pF
0V = 6.1kHz
5V = 4.7kHz
10V = 34kHz
Note that at 10V all of the outputs are at their max (I_abc is 1.38mA) so tracking is off. But all filters reach well above 20kHz. If one aims for a 40k cutoff 240pF and 270pF seem equally suited.
I have tried various cap values as well, and today I made a comparison of both cap values and changes to the expo converter.
Expo converter
The expo converter core is dependent on a reference current. Right now that is set up using a 1.5MOhm resistor, but changing this does not change the output curve, it only changes WHAT linear CV gives what output.
I tried swapping for a 1MOhm resistor, and using the base octave trimmer I could still get the necessary output range. Here are the currents through a single I_abc resistor:
Using 1.5MOhm resistor, the output current is:
Full trim and 5V CV range: 3.2nA to 1.377mA
Center trimmed: 165nA to 168uA
Using 1MOhm resistor, the output current is:
Full trim and 5V CV range: 4.9nA to 1.379mA
Center trimmed: 248nA to 238uA
The center trimmed range is well within the total range independent of resistor, with room to spare for additional octaves.
Filter caps
The Juno 106 uses 240pF caps, other Roland synths use 330pF, and we use 270pF. Here are the responses to a center trimmed CV using a 1.5MOhm reference resistor:
240pF
0V = 7.7Hz
5V = 6.4kHz
10V = 42kHz
270pF:
0V = 7Hz
5V = 5.7kHz
10V = 39kHz
0V = 6.1kHz
5V = 4.7kHz
10V = 34kHz
Note that at 10V all of the outputs are at their max (I_abc is 1.38mA) so tracking is off. But all filters reach well above 20kHz. If one aims for a 40k cutoff 240pF and 270pF seem equally suited.
Juno filter: VCA and Resonance CV circuit tweaking
I took a closer look at the Juno 106 circuit for VCA and Resonance CV to figure out what they did to the base-emitter voltage drop in the transistors in the circuit. While simulating it turned out that it actually uses a 10V resonance CV where I put 5V. This confirms my initial testing where I had to use 10V resonance CV to get a proper response.
Anyway, following the tuning instructions in the Juno 106 results in a response where the first 150mV of the CV does not output any I_abc current, because the transistor does not switch on until it sees a high enough voltage. This is practical as it will fully turn off the VCA. In my Xonik VCA I have assumed that 0V CV cuts off the output current, but if there are small differences in the supply lines or something we may still get a tiny output. The Juno does not have this problem because of the 'deadband'.
After calibrating the trimming I tested the current outputs:
VCA:
max -301uA
Resonance:
max -205 to -356 uA depending on the trimmer.
I wanted to add a mixing point for the VCA CV. I am not quite sure how to do this on the existing design - I could possibly add a resistor to the positive input of the VCA CV op amp - so I decided to use the current converter from the Xonik VCA.
Using standard component values, I ended up with this version
which has the following params:
VCA:
max -320uA
Resonance:
max -147 to -405
If trimming the size of the deadband is not necessary, the trimmer and 1MEG resistor may be replaced with a 1.5MEG resistor to -15V. This will give a deadband of about 150mV.
Leaving out the 1MEG resistor will give 0 current at 0V but with the possibility of a tiny current leakage, slightly turning on the VCA.
Frequency CV
I also modified the Frequency CV mixer a bit, now the trimmer lets you add or subtract up to 5.6 octaves.
As a side note, the 390k resistor to -15V adds 3.8V to the output. Switching the resistor from the trimmer from 270k to for example 150k would give the same trimability and remove the need for the 390k, but makes the trimmer slightly more sensitive.
Here is the updated circuit. I still want to add linear FM of the filter cutoff, but other than this I am getting close to a version that can be tested.
 |
| Juno 106 VCA CV |
Anyway, following the tuning instructions in the Juno 106 results in a response where the first 150mV of the CV does not output any I_abc current, because the transistor does not switch on until it sees a high enough voltage. This is practical as it will fully turn off the VCA. In my Xonik VCA I have assumed that 0V CV cuts off the output current, but if there are small differences in the supply lines or something we may still get a tiny output. The Juno does not have this problem because of the 'deadband'.
 |
| CV vs I_abc (red) before calibration - notice deadband at the start of I_abc |
 |
| CV vs I_abc after calibration, deadband ends at about 150mV |
 |
| CV vs voltage at opamp output - notice that we get 10V at the start. |
VCA:
max -301uA
Resonance:
max -205 to -356 uA depending on the trimmer.
I wanted to add a mixing point for the VCA CV. I am not quite sure how to do this on the existing design - I could possibly add a resistor to the positive input of the VCA CV op amp - so I decided to use the current converter from the Xonik VCA.
Using standard component values, I ended up with this version
which has the following params:
VCA:
max -320uA
Resonance:
max -147 to -405
If trimming the size of the deadband is not necessary, the trimmer and 1MEG resistor may be replaced with a 1.5MEG resistor to -15V. This will give a deadband of about 150mV.
Leaving out the 1MEG resistor will give 0 current at 0V but with the possibility of a tiny current leakage, slightly turning on the VCA.
Frequency CV
I also modified the Frequency CV mixer a bit, now the trimmer lets you add or subtract up to 5.6 octaves.
As a side note, the 390k resistor to -15V adds 3.8V to the output. Switching the resistor from the trimmer from 270k to for example 150k would give the same trimability and remove the need for the 390k, but makes the trimmer slightly more sensitive.
Here is the updated circuit. I still want to add linear FM of the filter cutoff, but other than this I am getting close to a version that can be tested.
Sunday, January 13, 2019
Juno filter with higher possible cutoff
While trying to find a suitable 0-5V CV filter range I discovered that my design had some unfortunate limitations.
The maximum cutoff achievable was around 16kHz. I tracked this down to two factors: The 220k resistor from the VCA-OTA output to ground and the output filter capacitor (fixed low pass filter). Removing the output cap helped a lot, but I still could not get higher than 30kHz cutoff independent of control current.
I still had to change the resistor, which meant I could not get proper unity amplification at 5V CV. Compensating elsewhere in the circuit (input buffer or pre-OTA) distorted the signal at my wanted 10V p.p. amplitude (while such a distortion may be desireable, I want control over it and it was not something I planned now).
I switched back to the original design with a 47k output resistor. Then I thought, I can compensate for the loss using additional output amps. I added two inverting amps (to keep the output in phase) and this worked well.
From my previous experiments I knew that I could replace the resistor-to-ground feeding a buffer, into an inverting amp with the same resistor in the feedback loop. Doing this meant I would only need a single additional opamp to get phase correction and unity gain. But doing his also had a surprising effect - distortion and cutoff was immediately improved!
Using this and a constant current input to the OTAs let me run the filter up to at least 130kHz. This is completely unrealistic though, as it would require a higher control current I_abc for the OTAs than they can handle (max is 2mA), but past 60kHz could be achievable
I then re-added the expo converter and got a surprise/reminder. I still couldn't push the filter past 24kHz. I simply could not get a control current higher than about 760uA. After trying a few adjustments in the exponential converter itself (changing reference current and emitter resistor) I turned to my exponential converter simulator and quickly discovered the problem - the current is controlled by changing the voltage drop across the resistor connected to the OTAs control pin. The pin is always around -13.3V in the simulator, and the transistor pulls its collector further and further away from this to generate a higher and higher current. But at about one diode drop above 0V it cannot go any further, it simply cuts off.
So, to get a higher current than this, I had to reduce the resistor value (remember, U=R*I, to get a higher I from the same U, R must decrease).
Doing this let me generate up to 1.38mA, putting the cutoff close to 40kHz.
Note that I have NOT tried to tune tracking when using the expo converter, it is possible that one could get a lot better tracking than this by adjusting U15. It is however also possible that there is something that prevents the expo converter from getting a perfect tracking over the full frequency range.
The maximum cutoff achievable was around 16kHz. I tracked this down to two factors: The 220k resistor from the VCA-OTA output to ground and the output filter capacitor (fixed low pass filter). Removing the output cap helped a lot, but I still could not get higher than 30kHz cutoff independent of control current.
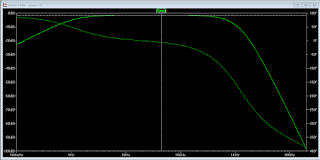
 |
| Cutoff is max 30kHz and has very poor tracking at high frequencies. Current is the total current for all four OTAs, divide by 4 to get I_abc |
I still had to change the resistor, which meant I could not get proper unity amplification at 5V CV. Compensating elsewhere in the circuit (input buffer or pre-OTA) distorted the signal at my wanted 10V p.p. amplitude (while such a distortion may be desireable, I want control over it and it was not something I planned now).
I switched back to the original design with a 47k output resistor. Then I thought, I can compensate for the loss using additional output amps. I added two inverting amps (to keep the output in phase) and this worked well.
From my previous experiments I knew that I could replace the resistor-to-ground feeding a buffer, into an inverting amp with the same resistor in the feedback loop. Doing this meant I would only need a single additional opamp to get phase correction and unity gain. But doing his also had a surprising effect - distortion and cutoff was immediately improved!
Using this and a constant current input to the OTAs let me run the filter up to at least 130kHz. This is completely unrealistic though, as it would require a higher control current I_abc for the OTAs than they can handle (max is 2mA), but past 60kHz could be achievable
 |
| Max cutoff is above 130kHz (though this would break the OTAs) and tracking is near perfect. |
Increasing range
I then re-added the expo converter and got a surprise/reminder. I still couldn't push the filter past 24kHz. I simply could not get a control current higher than about 760uA. After trying a few adjustments in the exponential converter itself (changing reference current and emitter resistor) I turned to my exponential converter simulator and quickly discovered the problem - the current is controlled by changing the voltage drop across the resistor connected to the OTAs control pin. The pin is always around -13.3V in the simulator, and the transistor pulls its collector further and further away from this to generate a higher and higher current. But at about one diode drop above 0V it cannot go any further, it simply cuts off. |
| Plotting the voltage at the right collector of circuit A shows that it cuts off above at approx 0.63mV. |
So, to get a higher current than this, I had to reduce the resistor value (remember, U=R*I, to get a higher I from the same U, R must decrease).
Doing this let me generate up to 1.38mA, putting the cutoff close to 40kHz.
 |
| Changing to a 10k resistor increases the maximum current. |
Tracking using the expo converter
Note that I have NOT tried to tune tracking when using the expo converter, it is possible that one could get a lot better tracking than this by adjusting U15. It is however also possible that there is something that prevents the expo converter from getting a perfect tracking over the full frequency range.
Output lowpass filter
I've added a 22pF output filter cap in, which seems to give a cutoff around 50kHz. This affects the tracking at high frequencies a bit too, so I'll have to do some testing.New circuit
Final notes
I do not know if changing the max cutoff frequency or the output lowpass filter affects the sound. It is possible that this messes with the Juno sound. Maybe the cutoff should not go as high (though the manual says 5-50kHz or 4-40kHz). I like try it at least. One could also squeeze out an even higher cutoff by reducing the resistor even further. The OTA control pin is at -13.3V in the simulator but it could perhaps be even lower in the circuit, but never less than the negative supply (-15V). The transistor never gets past about 0.7V. This means the overall range will be below 16V. As maximum I_abc is 2mA we COULD use an 9.1kOhm resistor and get max I_abc 1.75mA (or an 8.2kOhm and get 1.95mA, but then we are really close to theWednesday, January 2, 2019
Breadboarding the Juno filter
Tuesday, January 1, 2019
A closer look at the responses of the jp6 filter after fixing CV and bug
To make a good state variable filter with 12/24dB HP, LP and 12dB BP I simulated the JP6 filter and tapped it at various places to look at the responses.
For my simulated circuit, setting cutoff CV to 1.35 to get results comparable to my previous erroneous circuit. Resonance CV control is still a bit wonky but now it uses an expo converter. I have set reso to 0.5V (but there is a missing current limiting resistor in the circuit) to get 13dB resonance.
24dB LP:
- Cutoff: 500Hz
- Resonance: 13dB at 1.24kHz
24dB HP:
- Cutoff 3.2kHz
- Resonance: 13.2dB at 1.4kHz
12dB LP + 12dB HP,
12dB HP + 12 dB LP
- LP cutoff: 2.6kHz
- HP cutoff: 694Hz
- Center: 1.33kHz
- 13.4dB attenuation on top
- Resonance: Top has 1.1dB amplification
12dB LP with connection to second stage
- Cutoff: 772Hz
- Base attenuation 1.44dB
- Resonance: Top has 6.6dB amplification over base at 1.25kHz, base is -13dB
12dB LP without connection to second stage
- Cutoff: 769Hz
- Base amplification 1.4dB
- Resonance: Top has 6.6dB amplification over base at 1.25Hz, base is -10dB
12dB HP with connection to second stage
- Cutoff: 2.1kHz
- Base attenuation 1.7dB
- Resonance: Top has 6.4dB amplification over base at 1.4kHz, base is -13dB
12dB HP without connection to second stage
- Cutoff: 2.1kHz
- Base amplification 1.1dB
- Resonance: Top has 6.65dB amplification over base at 1.4kHz, base is -10dB
BTW: I have found another serious issue. The cap on the output amp prevents the filter from getting a higher LP cutoff than 14k. removing it gives a cutoff of about 20kHz at most. This does not seem right compared to the promised 5-50kHz in the datasheet.
For my simulated circuit, setting cutoff CV to 1.35 to get results comparable to my previous erroneous circuit. Resonance CV control is still a bit wonky but now it uses an expo converter. I have set reso to 0.5V (but there is a missing current limiting resistor in the circuit) to get 13dB resonance.
24dB LP:
- Cutoff: 500Hz
- Resonance: 13dB at 1.24kHz
24dB HP:
- Cutoff 3.2kHz
- Resonance: 13.2dB at 1.4kHz
12dB LP + 12dB HP,
12dB HP + 12 dB LP
- LP cutoff: 2.6kHz
- HP cutoff: 694Hz
- Center: 1.33kHz
- 13.4dB attenuation on top
- Resonance: Top has 1.1dB amplification
12dB LP with connection to second stage
- Cutoff: 772Hz
- Base attenuation 1.44dB
- Resonance: Top has 6.6dB amplification over base at 1.25kHz, base is -13dB
12dB LP without connection to second stage
- Cutoff: 769Hz
- Base amplification 1.4dB
- Resonance: Top has 6.6dB amplification over base at 1.25Hz, base is -10dB
12dB HP with connection to second stage
- Cutoff: 2.1kHz
- Base attenuation 1.7dB
- Resonance: Top has 6.4dB amplification over base at 1.4kHz, base is -13dB
12dB HP without connection to second stage
- Cutoff: 2.1kHz
- Base amplification 1.1dB
- Resonance: Top has 6.65dB amplification over base at 1.4kHz, base is -10dB
BTW: I have found another serious issue. The cap on the output amp prevents the filter from getting a higher LP cutoff than 14k. removing it gives a cutoff of about 20kHz at most. This does not seem right compared to the promised 5-50kHz in the datasheet.
Subscribe to:
Comments (Atom)